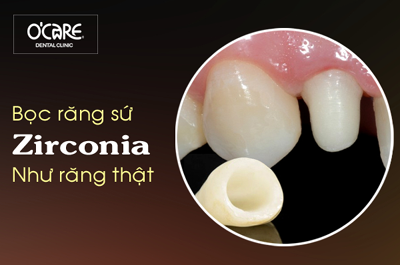
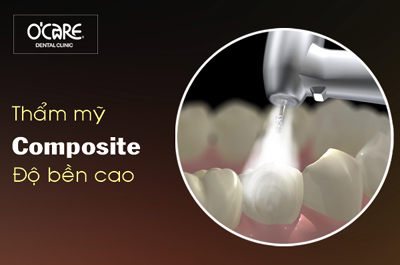
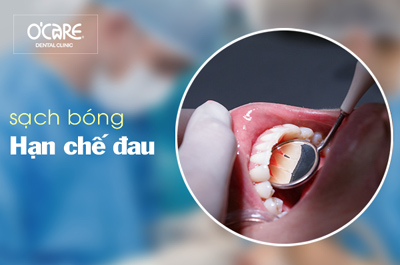
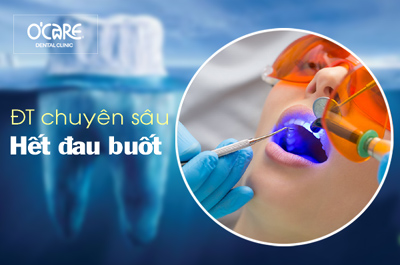
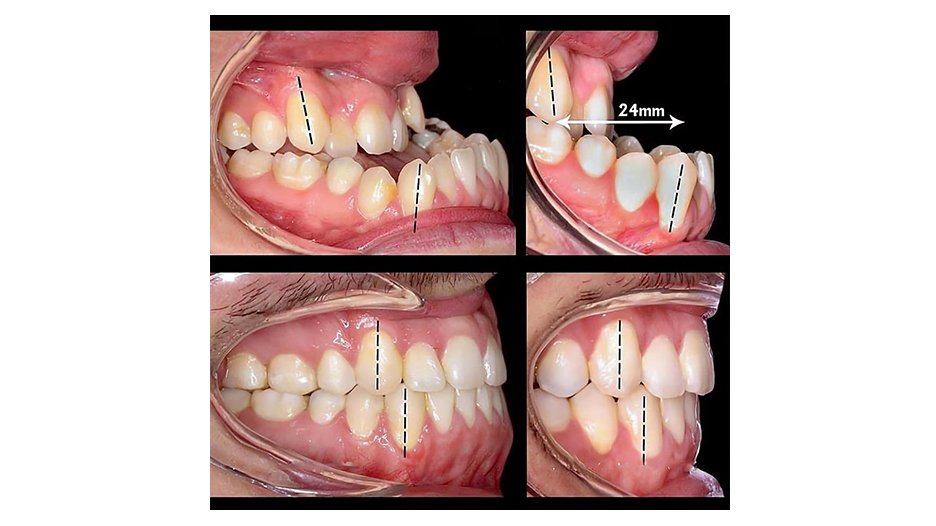
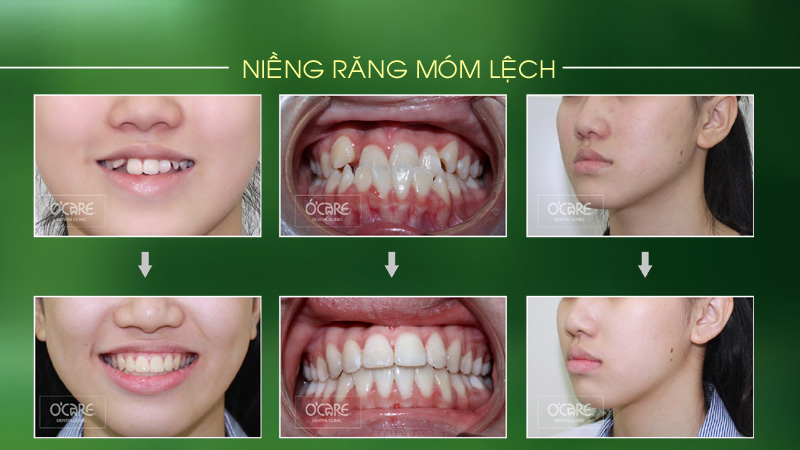
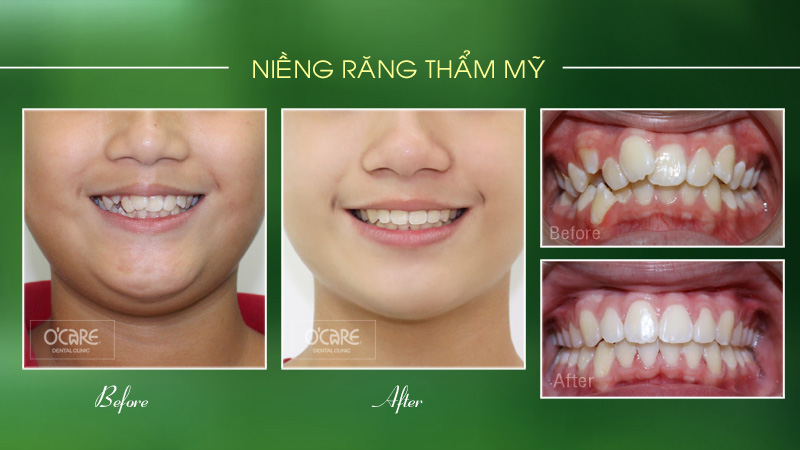
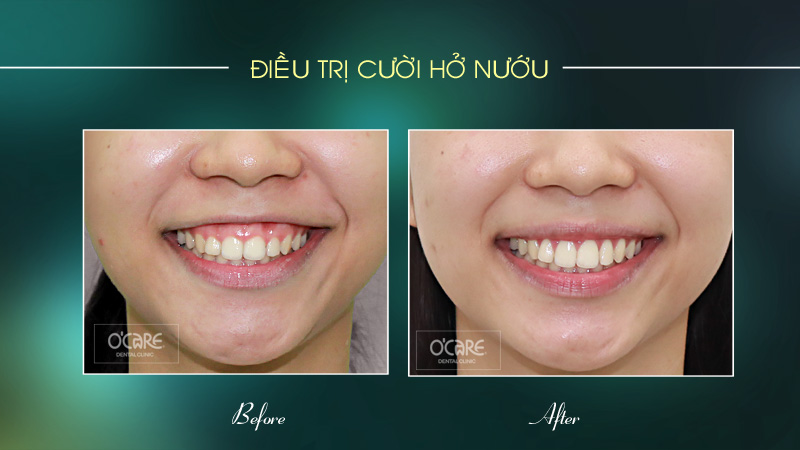
Tin tức & Sự kiện
-
 Thông báo lịch nghỉ lễ 30/4 & 1/5
Thông báo lịch nghỉ lễ 30/4 & 1/5
-
 Nha khoa O’Care thông báo lịch làm việc & nghỉ lễ Giỗ Tổ Hùng Vương
Nha khoa O’Care thông báo lịch làm việc & nghỉ lễ Giỗ Tổ Hùng Vương
-
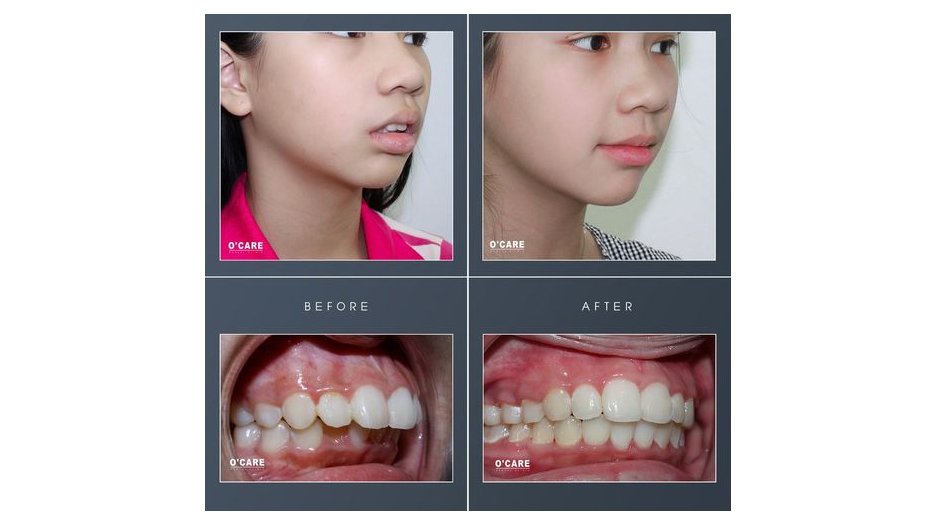
 Nha khoa O’Care Hà Nội đồng hành cùng sinh viên trường Đại học Lao động – Xã hội trên hành trình chăm sóc sức khỏe và thẩm mỹ nụ cười
Nha khoa O’Care Hà Nội đồng hành cùng sinh viên trường Đại học Lao động – Xã hội trên hành trình chăm sóc sức khỏe và thẩm mỹ nụ cười
-
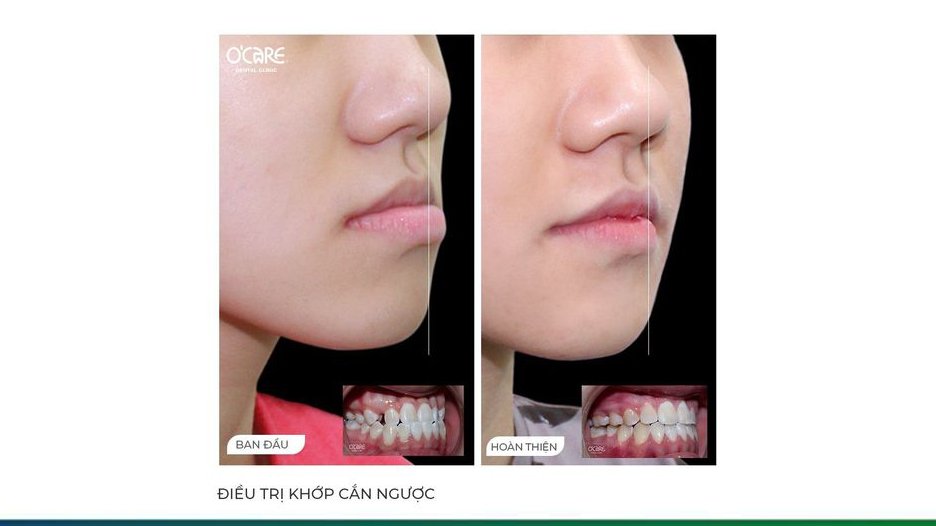
 Nha khoa O’Care tham dự lễ kỷ niệm 93 năm thành lập Đoàn TNCS Hồ Chí Minh tại trường Đại học Lao động – Xã hội
Nha khoa O’Care tham dự lễ kỷ niệm 93 năm thành lập Đoàn TNCS Hồ Chí Minh tại trường Đại học Lao động – Xã hội